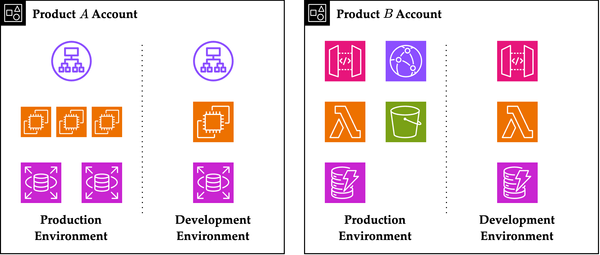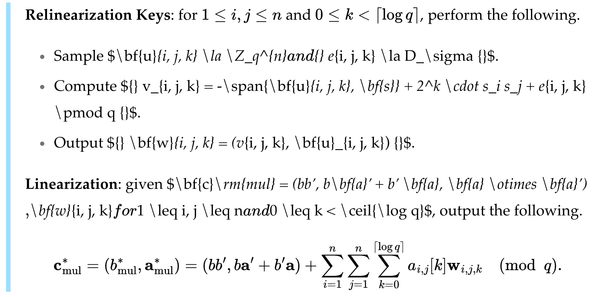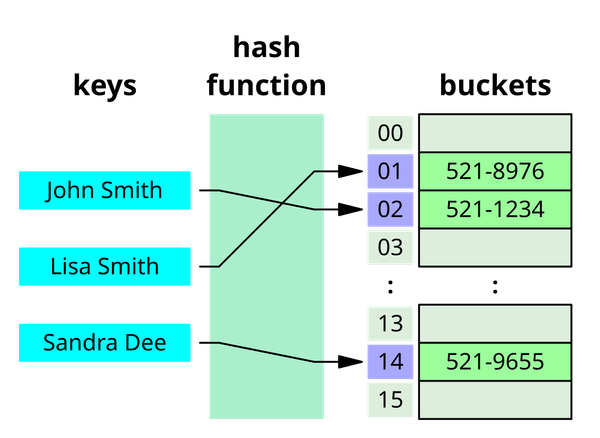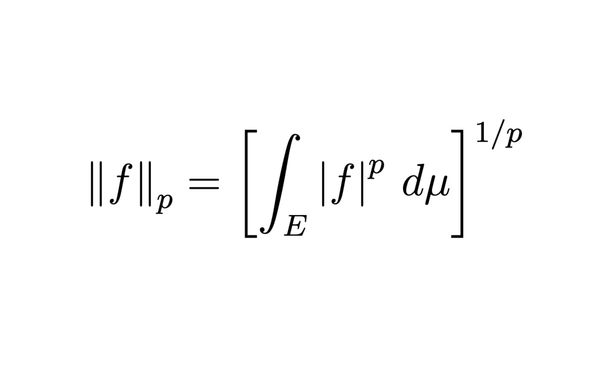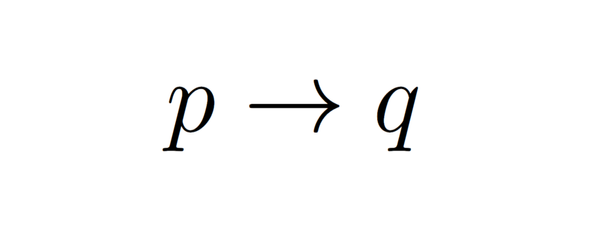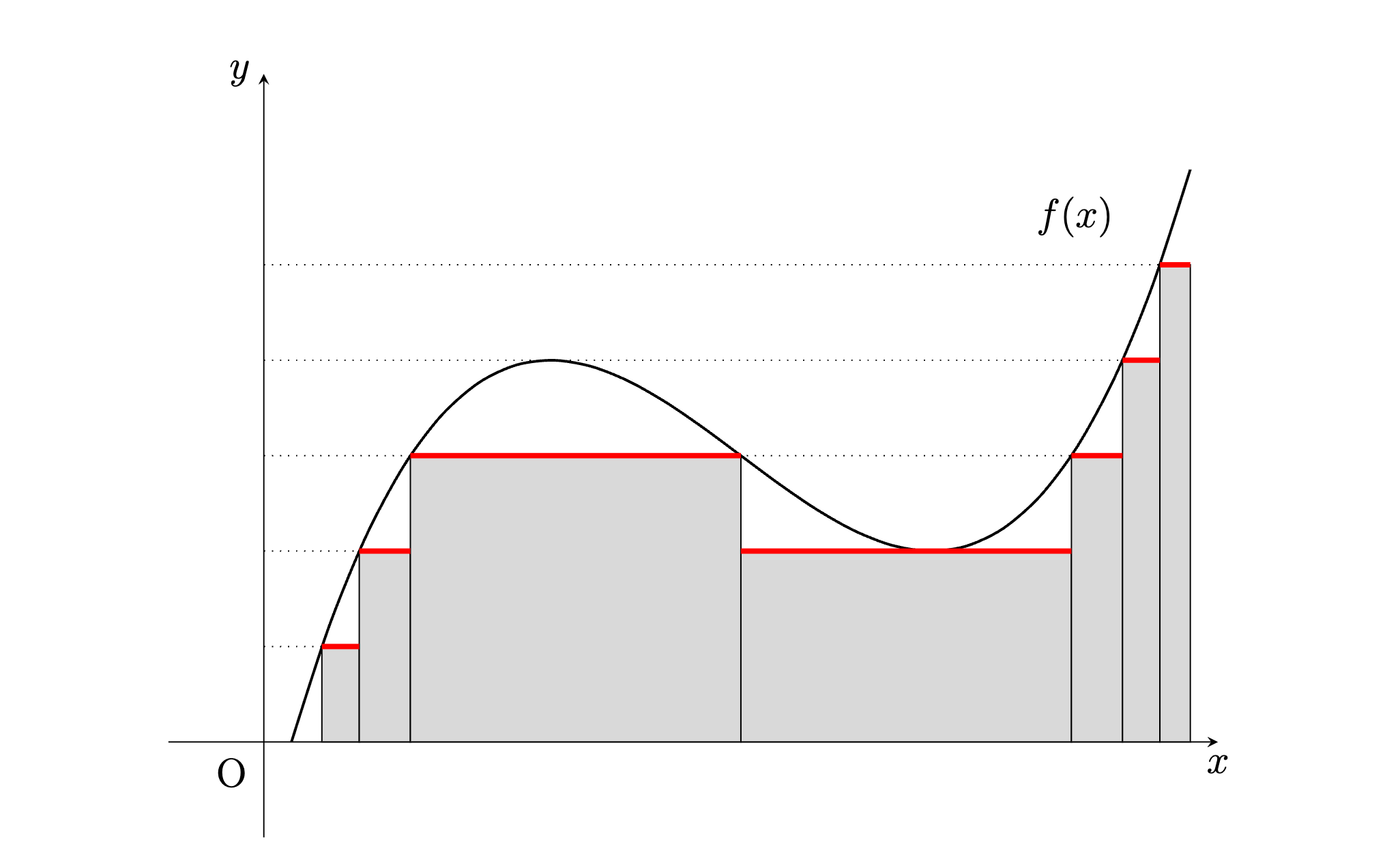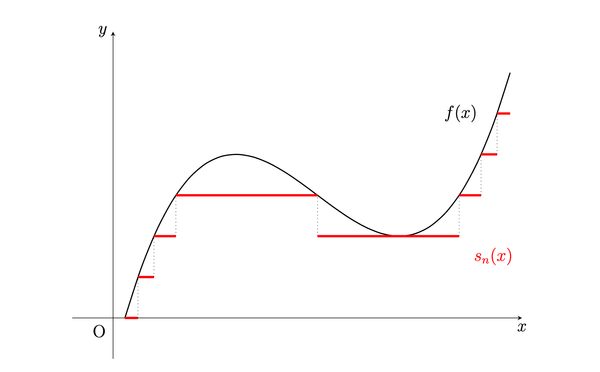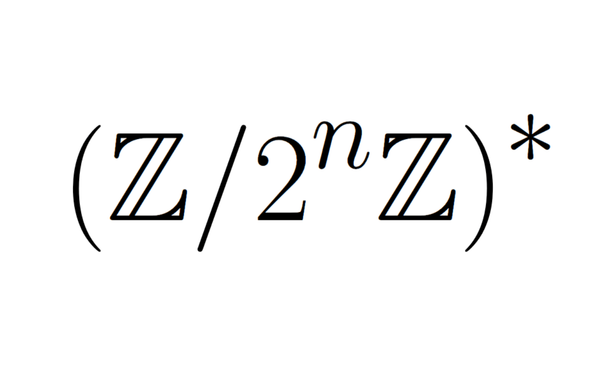
Group Structure of $(\mathbb{Z}/2^n \mathbb{Z})^*$
To compute the rotation automorphism homomorphically, we use the fact that $(\Z/2^n\Z)^* \simeq \span{-1, 5}$. I couldn't find a clear proof of this result online, so I just accepted the fact although it wasn't very satisfying. After more than a year, I